Needleman–Wunsch アルゴリズムはグローバルアラインメントを求めるアルゴリズムである。具体的な計算方法として、アラインメントを行う 2 つの配列を以下のように、碁盤のように縦と横に並べて配置する。例えば ATTGC と ATGC のアラインメントを求める場合は、下図のように並べる。
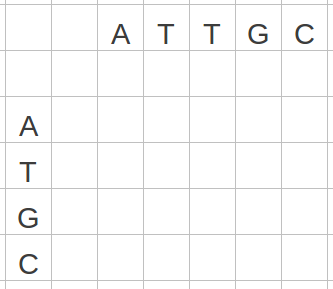
アラインメント、つまり 2 つの配列を「都合よく」合わせるためには、様々な制限を付ける必要がある。「都合よく」合わせるためには、例えば、「塩基 A と塩基 C 」が対応するよりも「塩基 A と塩基 A 」が対応した方がいい、といったルールが必要である。機械的にこのルールを実現するにはスコアと呼ばれるものを定義する必要がある。
2 つの配列を並べた時、各位置における塩基は 3 通りの状況が考えられる。
- 2 つの配列を並べた時、位置 p にある 2 つの塩基が一致する場合。(マッチ)
- 2 つの配列を並べた時、位置 p にある 2 つの塩基が不一致する場合。(ミスマッチ)
- 2 つの配列を並べた時、位置 p において、片方の配列の塩基に対して、もう片方の配列の塩基が存在しない場合。(ギャップ)
ここでは計算が簡単に行えるように、マッチの場合は +2 点、ミスマッチは -1 点、ギャップは -2 点と定義する。(スコアの定義は生物種や実験の目的などに応じて決める必要がある。)
以上のスコアの定義を文字式で書くと、s(A, A) = 2、s(A, B) = -1、 s(A, -) = s(-, A) = -2 となる(ただし、A, B は塩基であり、かつ、A ≠ B)。アラインメントは次のアルゴリズムに従って、1 格子ずつ計算する。なお、d はギャップがあったときのペナルティであり、定義により d = 2 である。
F(0, 0) = 0 として計算を進める。まず、F(1, 0)を計算する。
F(0, -1) および F(1, -1) は値が存在しないため、ここでは計算を行わない。そのため、F(1, 0) = F(0, 0) = -d = -2になります。同様にして計算を進め、F(n, 0) = -nd、F(0, n) = -nd が求まる。
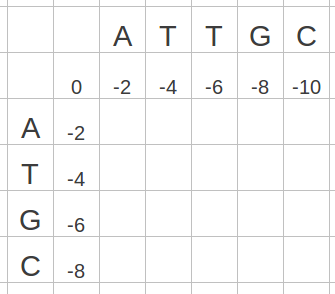
次に、F(1, 1) を求める。F(1, 1) の格子では、2 つの塩基がともに A であるから、スコアの定義により、s(A, A) = 2。また、ペナルティ d = 2 であるから、F(1, 1) は以下のように計算される。
F(1, 1) = F(0, 0) + 2 で計算されたものが最もスコアが高いことがわかる。以下のように、F(1, 1) のスコアを 2 とし、そのスコアは F(0, 0) から計算されていることがわかるように矢印を描き入れる。
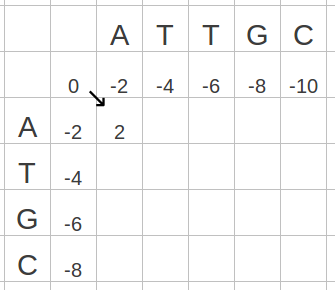
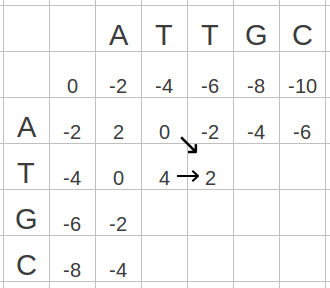
このように、格子を 1 つずつ計算していく。例えば、F(3, 2) の値については、次のように計算できる。
F(3, 2) が最大値を与えるのは F(2, 1) と F(2, 2) の 2 つが確認できる。 この場合、下図のように両方に矢印を描き入れておく。(※下図では、F(3, 2) への道のりがわかりやすいように、それ以外の矢印を省略した。)
最後の格子まで計算し終えたときの値がグローバルアラインメントのスコアとなる。この例では 6 となった。)
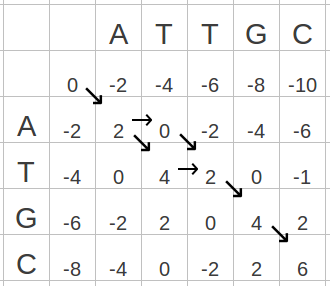
そこで、グローバルアラインメントを作成するには、図に記録した矢印に従って、矢印方向をさかのぼることでアラインメントを作成する。
# alignemnt 1 (score: 6)
ATTGC
AT-GC
# alignment 2 (score: 2)
ATTGC
A-TGC