生命情報科学

TMM 正規化

Trimmed mean of M values (TMM) 正規化は、RNA-seq のリードカウントデータを正規化する方法の一つである。細胞内で発現している遺伝子は、ハウスキーピング遺伝子などのような発現変動のない遺伝子（非発現変動遺伝子）が多いことに着目した正規化法である。

例えば 2 群間比較を考えたとき、非発現変動遺伝子の発現量は、2 つの実験群においてその対数比（M 値）はゼロになると期待される。しかし、何らかの技術的な原因などにより、その M 値の期待値がゼロとかけ離れる場合がある。TMM 正規化法は、非発現変動遺伝子の M 値の期待値をゼロに持っていくような係数を計算している。この係数のことを正規化係数（normalization factor）という。非発現変動遺伝子の M 値の期待値がゼロでないデータに、この正規化係数を作用させることで、その期待値が（理論上）ゼロになる。

例えば、以下の腎臓と肝臓 (Marioni et al.) の M-A plot でみられるように、正規化前ではハウスキーピング遺伝子の M 値の mean が -0.845 であるのに対して、TMM 正規化後は -0.249 となった。プロットを眺めると、すべての点が y 軸方向に +0.596 だけシフトしていることがわかる。正規化係数はこのように y 軸（= M 値 = 対数比）におけるシフトの程度を意味する。

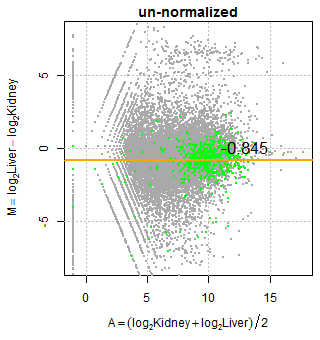
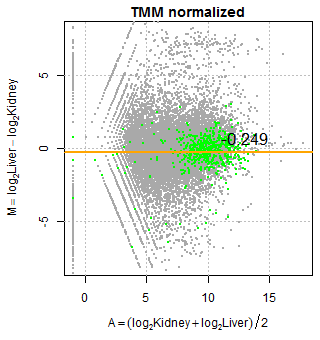
正規化前のmarioniのデータのMAplot TMM正規化後のmarioniのデータのMAplot

TMM 正規化法

edgeR に実装されている TMM 正規化（正規化係数の計算方法）は以下の手順で行われる。

  1. すべての遺伝子について M 値と A 値を計算する。
  2. すべての M 値について、上位 30% と下位 30% を除去する。
  3. すべての A 値について、上位 5% と下位 5% を除去する。
  4. 残ったデータを利用して正規化係数を計算する。

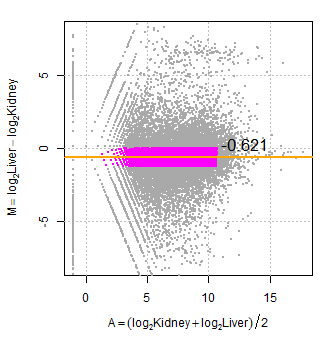
M 値と A 値に基いてトリムしたあとに残ったデータは、下図のマゼンダ色の点で表している。正規化係数はこれらのマゼンダ色から計算される。マゼンタ色の遺伝子の mean が -0.621 であるから、M-A プロットでいうと、これがゼロとなるように y 軸方向の +0.621 だけシフトさせるような係数を計算する。e

TMM正規化法のトリーム領域

M 値および A 値の求め方

遺伝子 g = 1, 2, 3, ..., G について、M 値及び A 値は次のように計算される。

\[ \begin{eqnarray} M_{g} &=& \log_{2}\frac{\left( \frac{Y_{gk}}{N_{k}}\right)}{\left(\frac{Y_{gl}}{N_{l}}\right)} \\ A_{g} &=& \frac{\log_{2}\left( \frac{Y_{gk}}{N_{k}}\times\frac{Y_{gl}}{N_{l}} \right)}{2} \end{eqnarray} \]

ここで、Ygkはライブラリー k の遺伝子 g のリードカウントデータを表す。また、Nk はライブラリー k のライブラリーサイズを表す（Nk = Σg=1GYgk）。

TMM 正規化係数の求め方

M 値および A 値に基いてトリムしたあとに残ったデータを利用して計算する。ライブラリー k の正規化係数はライブラリー r を対照群として次のように計算する。

\[ \log_{2}(TMM_{k}^{r}) = \frac{\sum_{g=1}^{G}w_{gk}^{r}M_{gk}^{r}}{\sum_{g=1}^{G}w_{gk}^{r}} \] \[ w_{gk}^{r} = \frac{N_{k} - Y_{gk}}{N_{k}Y_{gk}} + \frac{N_{r}-Y_{gr}}{N_{r}Y_{gr}} \]

TMM 正規化と多群間比較について

TMM 正規化はハウスキーピング遺伝子などの非発現変動遺伝子の log-fold-change をゼロにシフトさせる方法である。二つのライブラリーを比較して、そのシフトする程度となる TMM 正規化係数を計算する。二つのライブラリーというのは、「肝臓 vs. 腎臓」を意味しているだけではなく、「肝臓1 vs 肝臓2」でも構わない。2 群間の場合、肝臓サンプルが三つの biological replicate があり、腎臓も同様に三つの biological replicate あると仮定した時、TMM 正規化係数は次のように計算される。

  1. 6 biological replicate それぞれに対して upper quartile を計算し、upper quartile が最も小さいライブラリーをリファレンスライブラリーとする。
  2. リファレンスライブラリーと残りのライブラリーそれぞれに対して、正規化係数を求める。ここで、残りの 5 ライブラリーそれぞれに対して正規化係数が求まる。なお、リファレンスライブラリーの正規化係数は 1 である。
  3. 最後に、正規化係数の平均を揃える処理を行う。

この操作からして、正規化係数を計算するとき、肝臓か腎臓かをそもそも配慮していない。あくまで「リファレンスライブラリー vs. その他のライブラリー」である。二群間であろうか、多群間であろうか、この正規化法では実験デザインを考慮してなく、あくまで「リファレンスライブラリー vs. その他のライブラリー」で正規化係数を算出している。

References

  • Robinson MD, Oshlack A. A scaling normalization method for differential expression analysis of RNA-seq data. Genome Biol. 2010, 11(3):R25. PubMed Abstract
  • Marioni JC, Mason CE, Mane SM, Stephens M, Gilad Y. RNA-seq: an assessment of technical reproducibility and comparison with gene expression arrays. Genome Res. 2008, 18(9):1509-17. PubMed Abstract
  • Eisenberg E, Levanon EY. Human housekeeping genes are compact. Trends Genet. 2003, 19(7):362-95. PubMed Abstract