マイクロアレイあるいは RNA-Seq を用いた解析で、多数のサンプル(またはライブラリー)を対象としているとき、サンプル同士の類似度を調べたい場合がある。サンプル間の 類似度を調べる方法としてはクラスタリングや主成分分析(PCA)などの方法が挙げられる。ここで乱数の生成により作成したデータを利用して PCA を行う方法を示す。
サンプルデータ
サンプルデータは条件を設定して負の二項分布に従うように乱数生成により作成した。A 群と B 群の 2 つの実験群からなる。A 群には薬剤 A を投与し、0 時間、3 時間、6 時間の 3 つの時刻においてサンプルを採取した。B 群には薬剤 B を投与し、0 時間、3 時間、6 時間の 3 つの時刻においてサンプルを採取した。各実験の各時刻において 2 つの biological replicate があり、実験全体で計 12 biological replicate を使用したとする。また、全遺伝子数は 1,000 とした。サンプルデータを読み込んでから行列型に変換し、count 変数に代入する。
count <- read.table("https://bi.biopapyrus.jp/data/counts_6_6_timecourse.txt", sep = "\t", header = T, row.names = 1)
count <- as.matrix(count)
dim(count)
## [1] 1000 12
head(count)
## A1_0h A2_0h A3_3h A4_3h A5_6h A6_6h B1_0h B2_0h B3_3h B4_3h B5_6h B6_6h
## gene_1 1 7 11 0 22 24 0 0 9 3 22 16
## gene_2 170 182 744 683 918 637 128 112 645 517 1248 1234
## gene_3 8 12 37 46 100 94 9 8 30 46 47 63
## gene_4 44 38 109 187 354 225 40 97 103 146 505 343
## gene_5 0 0 5 0 4 10 0 0 1 0 7 4
## gene_6 88 112 372 459 1010 611 129 80 486 360 678 767一般的に、これらのデータを正規化した上で、分散の大きい遺伝子のみに対して、PCA を行う。ここで、簡略化のため、正規化しないですべての遺伝子に対して主成分分析を行う。
サンプル間の主成分分析
サンプル(ライブラリー)間同士の類似性を調べるのに、遺伝子発現量行列のサンプルを標本として、遺伝子を変数(属性)として(すなわち、サンプルが行、遺伝子が列からなる行列として)、主成分分析を行う。主成分分析は prcomp 関数で行い、入力データはすでに正規化後のデータであることから scale = FALSE とする。ただし、ここで注意しなければならないのは、一般的な発現量行列は、列がサンプル、行が遺伝子であるから、サンプル間の主成分分析を行うのにこの発現量行列の行と列を入れ替える必要がある。
count.log <- log10(count + 1)
pcaobj <- prcomp(t(count.log), scale = FALSE)なお、遺伝子同士の類似度を調べたいときは、遺伝子発現量行列の行と列を入れ替える必要はない。
寄与率
寄与率は、遺伝子発現量データの全情報量のうち、該当の主成分が占める情報量の割合を表す。寄与率は、標準偏差 pcaobj$sdev から計算できる。
v <- pcaobj$sdev ^ 2
v / sum(v)
## [1] 1.767198e-01 1.347773e-01 9.563106e-02 8.823813e-02 8.633609e-02 8.045111e-02 7.823496e-02 7.185369e-02 6.871914e-02 6.220043e-02 5.683828e-02 1.591822e-31寄与率から、第 1 主成分だけでデータの全情報量のうち 17.7% を説明でき、第 2 主成分だけでデータの全情報量のうち 13.5% を説明できる、ことが読み取れる。
主成分得点
主成分得点は、データを、主成分軸をもとに回転させた結果(座標情報)を表す。pcaobj$x にデータが保存されている。
head(pcaobj$x)
## PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8 PC9 PC10 PC11 PC12
## A1_0h -3.9824684 0.4189787 -1.695064 2.2690648 0.7114404 0.5047972 1.6383645 5.4063408 -1.3112757 1.1497244 3.70722373 1.356771e-15
## A2_0h -5.1831553 -0.5226985 -3.012980 -0.8746029 -0.3553775 -1.1885264 -3.7807881 1.7753367 -0.7163036 1.0551335 -4.70231298 -9.187096e-15
## A3_3h 0.5706374 -5.6062917 3.188343 -2.0385918 2.8762906 1.2300692 -0.7388527 1.8241733 4.9753892 -0.2524763 0.03386147 1.008091e-15
## A4_3h 1.0245640 -4.7770524 4.102362 3.4108147 1.4596468 -1.4903989 0.4531101 -1.8144433 -4.2952441 1.8354609 -0.79739943 3.267704e-15
## A5_6h 4.2636544 -2.9353765 -3.794733 2.5773133 -1.8105817 -3.5980836 -1.6191003 -0.5477820 0.8852792 -3.8933904 1.37566630 -2.827599e-16
## A6_6h 5.0400482 -2.4332676 -1.254919 -3.4618195 -5.2593534 3.3858676 1.4888447 0.6823058 -1.5468897 1.6561593 -0.24609358 3.279495e-15
col <- c("red", "red", "red", "red", "red", "red", "blue", "blue", "blue", "blue", "blue", "blue")
time <- c("0", "0", "3", "3", "6", "6", "0", "0", "3", "3", "6", "6")
PC1 <- pcaobj$x[, 1]
PC2 <- pcaobj$x[, 2]
PC3 <- pcaobj$x[, 3]
plot(PC1, PC2, type = "n", asp = TRUE)
text(PC1, PC2, labels = time, col = col)
plot(PC2, PC3, type = "n", asp = TRUE)
text(PC2, PC3, labels = time, col = col)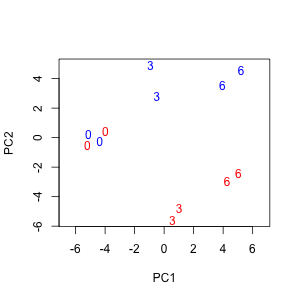
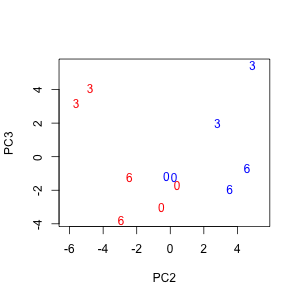
第 1 主成分をみると、A 群と B 群のサンプルは、時系列的に並んでいることが確認できる。薬剤投与後、時間が経つほど第 1 主成分の値(主成分得点)が大きくなっていく。また、第 2 主成分を見ると、0 時点では A 群と B 群のサンプルは互いに近いが、時間が経つほど、 A 群と B 群のサンプルが互いに離れていくのが確認できる。さらに第 3 主成分まで見ていくと、0 hr 時点のサンプルと 6 hr 時点のサンプルが似ていることが確認できる。
固有ベクトル
prcomp 関数で主成分分析を行うと、結果に固有ベクトルも保存される。固有ベクトルは pcaobj$ration に保存される。この固有ベクトルは、主成分得点だと勘違いして解析しないように注意すること。
head(pcaobj$rotation)
## PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8 PC9 PC10 PC11 PC12
## gene_1 0.10364426 0.025288523 -0.0350409756 -0.032754449 -0.03389323 0.003045047 -0.0710925659 0.067526610 0.071050099 -0.012216338 -0.045979424 0.15074286
## gene_2 0.08685768 0.008829570 0.0329951368 0.004400331 0.01501043 -0.026257883 -0.0241495762 0.009505452 0.015633351 0.006530217 -0.007834815 0.43104536
## gene_3 0.09030579 -0.011679298 0.0142918992 -0.019934536 -0.01855791 -0.035340836 -0.0144522304 -0.006131765 -0.003919578 -0.005139853 -0.004152529 -0.28504692
## gene_4 0.08849052 0.012237562 -0.0006667566 0.005403210 0.02379673 -0.001408423 -0.0003516202 -0.025851849 -0.015771146 -0.027266176 -0.000685528 -0.01082095
## gene_5 0.08970395 -0.006299658 -0.0188610082 -0.013513770 -0.01301046 0.045473615 -0.0110326977 0.018146169 0.059766220 0.004305710 -0.008146089 -0.34752065
## gene_6 0.09002338 0.004858552 0.0233055275 0.005159851 -0.01412885 -0.034610249 -0.0202140048 -0.013940280 0.015260773 -0.002193722 -0.002397592 -0.37132448