生命情報科学

階層クラスタリング

階層クラスタリングは、距離がもっとも短い 2 要素を 1 つのクラスタにまとめることを繰り返すことによって、すべての要素をクラスタリングする方法である。例えば、N 個の要素をクラスタリングする場合、まず、N 個のクラスタを作成し、1 クラスタに 1 つの要素を持つようにする。次に、N 個のクラスタに対して、クラスタ間を計算する。続いて、距離がもっとも短い 2 クラスタをまとめて 1 つのクラスタとする。ここまで、始めに N 個だったクラスタが N - 1 個となった。このような操作を、クラスタが 1 つだけになるまで繰り返す。このように求められたクラスタは、樹形図（系統樹）によって視覚化されるのが一般的である。

クラスタ間距離

クラスタ間距離は、様々な定義が使われている。有名なクラスタ間距離としては、最短距離法、最長距離法、群平均法、ウォード法がある。クラスタ Ci と Cj のクラスタ間距離を D(Ci, Cj) とおくと、これらの距離計算は以下のように計算できる。

最短距離法

2 つの要素 xi と xj の距離を d(xi, xj) とすると、最短距離法による距離計算は、次のように求めることができる。d(xi, xj) はユーグリッド距離、コサイン距離や相関係数などとすることができる。

\[ D(C_{i},C_{j})=\min_{\mathbf{x}_{i} \in C_{i},\mathbf{x}_{j} \in C_{j}}d(\mathbf{x}_{i},\mathbf{x}_{j})\]
set.seed(12345)
data <- matrix(rnorm(100), ncol = 10)
d <- dist(t(data), method = "euclidean")
h <- hclust(d, method = "single")
plot(h)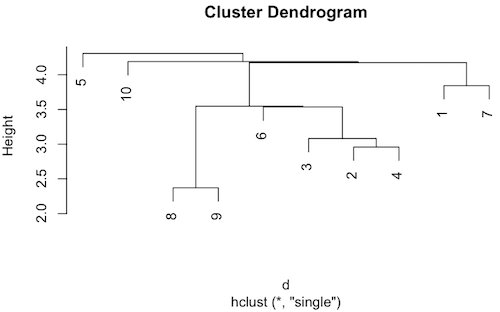
最短距離法によるクラスタリング結果

最長距離法

\[ D(C_{i},C_{j})=\max_{\mathbf{x}_{i} \in C_{i},\mathbf{x}_{j} \in C_{j}}d(\mathbf{x}_{i},\mathbf{x}_{j})\]
d <- dist(data, method = "euclidean")
h <- hclust(d, method = "complete")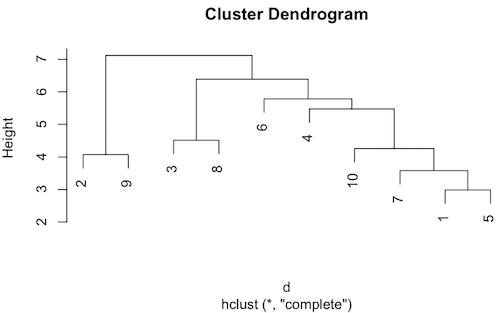
最長距離法によるクラスタリング結果

群平均法

\[ D(C_{i},C_{j}) =\frac{1}{|C_{i}||C_{j}|}\sum_{\mathbf{x}_{i}\in C_{j}}\sum_{\mathbf{x}_{j}\in C_{j}}d(\mathbf{x}_{i},\mathbf{x}_{j})\]
d <- dist(data, method = "euclidean")
h <- hclust(d, method = "average")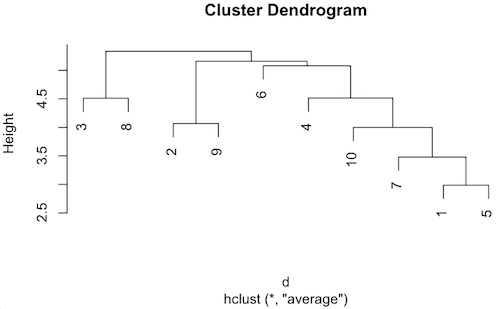
群平均法によるクラスタリング結果

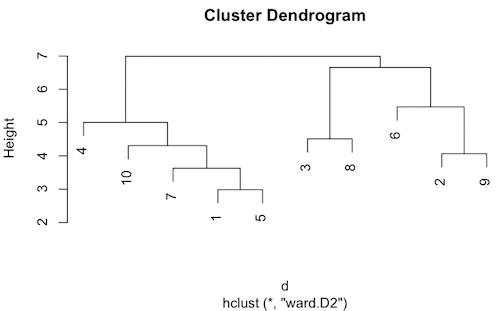
ウォード法

Ci と Cj のクラスタの要素数をそれぞれ ni と nj とし、xi と xj の中心をそれぞれ mi と mj とすると、ウォード法による距離計算は次のように求めることができる。

\[ D(C_{i},C_{j})=\frac{n_{i}n_{j}}{n_{i} + n_{j}}|| \mathbf{m}_{i} + \mathbf{m}_{j} ||^{2} \]

マイクロアレイのデータや RNA-Seq の FPKM などの遺伝子発現量をクラスタリングする際に、ウォード法を用いた方がきれいに別れる場合が多い。

d <- dist(data, method = "euclidean")
h <- hclust(d, method = "ward.D2")
ウォード法によるクラスタリング結果